压缩感知SL0图像重建算法的opencv实现

最近研究生的项目中涉及到压缩感知的SL0图像重建算法，需要对其进行C++实现。

按照压缩感知的理论框架，可以将它分为三个部分：图像的稀疏表示，即寻找一个正交基使原始图像尽可能的稀疏，图像的稀疏表示越充分，就越有利于图像的重建；测量矩阵的设计，为了重构稀疏信号，编码采样测量矩阵必须满足约束等距性RIP(Restricted isometry property)条件， 即将编码采样视为对原有信号的一种映射变换；图像重建，即通过测量信号重构原始信号。

重建算法相当于信号测量过程的逆过程，设一个长度为N的原始信号经过测量矩阵得到一个长度为M(M<N)的测量值信号，高分辨率成像重建的过程是通过测量向量y重构原始信号x的过程，由于方程个数远少于求解未知量个数，必须解一个欠定方程，很难直接求解。但由于原始信号是稀疏的或者能够稀疏表示，所以通常会加一个稀疏表达作为正则项，而稀疏表达通常用求解最小L0范数的方式加以表示，如下式所示：

$$
\hat{x}=\arg \min |x|_{0} \quad \text { s.t. } \quad \Phi x=y
$$

但求解最小L0范数通常很困难，是一个NP难问题，比如长度为N的稀疏信号中有K个非零值，则稀疏信号有$\mathrm{C}_{\mathrm{N}}^{\mathrm{K}}$种排列可能，要找到最接近于原始信号的最优排列，计算复杂度非常高。因此为了高分辨率成像重建的高效进行，常常会规避零范数问题，比如会选择以最小L1范数法为代表的次最优解算法以及以正交匹配追踪算法为代表的的贪婪算法进行求解，此外还常用迭代阈值法和最小全变分法。也可以用一种渐近逼近L0范数的高分辨率成像重建算法，通过渐近化解非凸优化求解的困难，通过L0约束确保信号的稀疏度。

信号重构算法是指由长度为M测量向量的y重构长度为N(M<N)的稀疏信号s的过程。

$$
\hat{\mathrm{s}}=\operatorname{argmin}|\mathrm{x}|_{0} \quad \text { s.t. } \mathrm{y}=\Theta \mathrm{s}
$$

项目中涉及到的SL0算法是由最小L2范数向最小L0范数的逐渐逼近，上式中Θ是传感矩阵，$|\mathrm{x}|_{0}$表示的是L0范数，研究首先定义一个逼近函数模型：

$$
\mathrm{f}{\sigma}(s)=1-\exp \left(-s^{2} / 2 \sigma^{2}\right) \quad \mathrm{f}{\sigma}\left(s{i}\right)=1-\exp \left(-s{i}^{2} / 2 \sigma^{2}\right)
$$

从而有$\mathrm{F}{\sigma}(\mathrm{s})=\sum{\mathrm{i}=1}^{\mathrm{n}} \mathrm{f}{\sigma}\left(\mathrm{s}{\mathrm{i}}\right)$，其中，n为稀疏信号向量s的长度，si为稀疏信号向量s对应的第i个元素，σ为逼近L0范数的调制参数，$\mathrm{F}{\sigma}(\mathrm{s})$近似表示s非零较大项的数目。逼近函数$\mathrm{f}{\sigma}\left(\mathrm{s}{\mathrm{i}}\right)$和$\mathrm{s}{\mathrm{i}}$、σ的关系如下图所示：

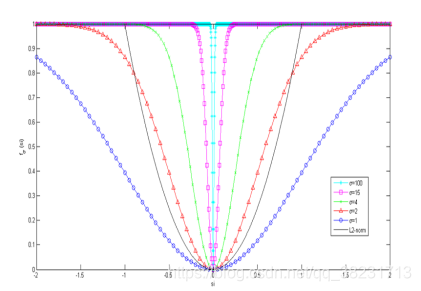
当σ较大时，$\mathrm{F}{\sigma}(\mathrm{s})$可以近似表示为L2范数。根据渐进思想，当σ取值逐渐减小时，$\mathrm{F}{\sigma}(\mathrm{s})$逐渐逼近L0范数，向量s的L0范数准则的优化问题可近似表示为$|\mathrm{s}|{0}=\mathrm{F}{\sigma}(\mathrm{s})$。另外从上图可知，由于逼近的L0范数的函数曲线是光滑可导的，因此被称为逼近光滑L0范数算法（简称为SL0）。

由此，稀疏表示$|\mathrm{x}|{0}$极小问题，转化为连续函数$\mathrm{F}{\sigma}(\mathrm{s})$的极小。从而重建式转化为一种全新的稀疏表示模型：

$$
\hat{\mathbf{s}}=\arg \min \mathrm{F}_{\sigma}(\mathrm{s}) \text { s.t } \Theta \mathrm{s}=\mathrm{y}
$$

此模型通常只针对于普通的稀疏表示，对于图像重构这一类的逆问题，稀疏表示通常用来作为先验正则项，所以为了求解图像重构问题的最优解，增加了一个重构逼近项的约束优化问题。在模型的基础上，增加了重构的残差项，进而形成了光滑L0范数稀疏表示加误差逼近的完整的压缩感知图像重构模型：

$$
\mathrm{J}(\mathrm{s})=\arg \min \left{\mathrm{F}{\sigma}(\mathrm{s})+\lambda|\Theta \mathrm{s}-\mathrm{y}|{2}^{2}\right}
$$

式中λ为权重平衡参数。上述模型中的稀疏表示先验项以稀疏信号s为处理内容，而误差逼近项是重构图像投影测量值与实际值的残差极小为整幅图像的全局优化。由于是逼近最小L0范数的算法求解方式，$\mathrm{F}{\sigma}(\mathrm{s})$中的σ参数是逐步减小的，因此逼近最小L0范数稀疏表示的优化问题可采用梯度下降的迭代计算方式来解决，即对式中s进行求导，在梯度方向$\Delta \mathrm{J}(\mathrm{s})$进行迭代：
$$
\Delta J(s)=d=2 \lambda\left(\Theta^{T}(\Theta s-y)\right)+\left(1 / \sigma^{2}\right)^{*}\left[s{1} \exp \left(-s{i}^{2} \sigma^{2} / 2\right), \cdots, s{m} \exp \left(-s_{m}^{2} \sigma^{2} / 2\right)\right]^{\mathrm{T}}
$$

基于梯度下降的逼近最小L0范数算法的伪代码过程如下：
1) 变量名的物理含义：传感矩阵Θ，测量值y，原始信号的稀疏表示s；
2) 初始化：$\hat{\mathrm{s}}{0}=\Theta^{\perp} \mathrm{y}, \Theta^{\perp}$为Θ的伪逆阵，$\Theta^{\perp}=\left(\Theta^{\mathrm{T}} \Theta\right)^{-1} \Theta^{\mathrm{T}}$，设增长序列$\sigma=\left[\sigma{1}, \ldots, \sigma{k}\right]$、λ和梯度下降步长µ；
3) 循环σ序列k：
a) $\sigma=\sigma{\mathrm{k}}, \quad \widehat{\mathrm{s}}=\widehat{\mathrm{s}}{\mathrm{k}-1}$；
b) 梯度下降法迭代L次：
a.梯度下降方向：
$$
d=2 \lambda\left(\Theta^{T}(\Theta s-y)\right)+\left(1 / \sigma^{2}\right)^{*}\left[s{1} \exp \left(-s{i}^{2} \sigma^{2} / 2\right), \cdots, s{m} \exp \left(-S{m}^{2} \sigma^{2} / 2\right)\right]^{\mathrm{T}}
$$b.梯度方向更新：$\widehat{\mathrm{s}}=\widehat{\mathrm{s}}-\mu \mathrm{d}$
c.约束正交投影：$\widehat{\mathrm{s}}=\widehat{\mathrm{s}}-\Theta^{\perp}(\Theta \widehat{\mathrm{s}}-\mathrm{y})$
c) $\hat{\mathrm{s}}{\mathrm{k}}=\hat{\mathrm{s}}, \quad \mathrm{k}=\mathrm{k}+1$；
4) 结束循环：输出$\widehat{\mathrm{s}}_{\mathrm{k}}$为最终求得的稀疏信号s。

值得注意的是，在算法求解过程中，随着迭代的进行，误差$|\Theta s-y|{2}^{2}$越来越小，使稀疏表示正则项$\mathrm{F}{\sigma}(\mathrm{s})=\sum{\mathrm{i}=1}^{\mathrm{n}} \mathrm{f}{\sigma}\left(\mathrm{s}{\mathrm{i}}\right)$越来越逼近于L0范数，同时可以让误差$|\Theta s-y|{2}^{2}$所占权重逐渐减小，逼近L0范数的稀疏表示正则项$\mathrm{F}{\sigma}(\mathrm{s})$所占权重逐渐增大。因此λ设置成递增序列，σ设置成递减序列，从而在迭代过程中可以根据误差$|\Theta s-y|{2}^{2}$的大小能够自适应地去调整λ和σ的值。

由逼近图可知，随着σ的逐渐减小，稀疏表示正则项$\mathrm{F}_{\sigma}(\mathrm{s})$越来越光滑地逼近近似的L0范数，在逐渐降低了重构稀疏信号的稀疏度的同时以更大效率逐渐逼近我们需要的全局最优解，从而降低了算法复杂度和提高了图像重建的精度，从而更加利于高分辨率图像的重建。

简单的实验验证

例如对于矩阵的乘法$\Theta^{*} \mathrm{s}=y$

$$
\left[\begin{array}{ccccc}{0.245} & {-0.053} & {4.478} & {-3.426} & {3.487} & {2.85} \ {-1.205} & {3.42} & {-2.39} & {-2.752} & {4.49} & {11.676}\end{array}\right] *\left[\begin{array}{c}{0} \ {0} \ {-8.361} \ {0} \ {0} \ {-12.982}\end{array}\right]=\left[\begin{array}{c}{-74.4383} \ {-131.5950}\end{array}\right]
$$

其中Θ为传感矩阵，s为原始信号在变换域中的稀疏表达，y为维度更低的测量信号。由2维的y来恢复6维的s是一个欠定问题，但如测量矩阵满足RIP条件，将s的稀疏性作为正则项，就有较大的概率重构出原始信号。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int main(int argc, char **argv)
{
	Mat A = (Mat_<double>(2, 6) << 0.245f, -0.053f, 4.478f, -3.426f, 3.487f, 2.85f, 
							       -1.205f, 3.42f, -2.39f, -2.752f, 4.49f, 11.676f);
	Mat y = (Mat_<double>(2, 1) << -74.4393f, -131.5950f);
	Mat s(6, 1, CV_64FC1);
	/*sigma_min为sigma迭代终止的条件，sigma_min越小，重构结果就越精确*/
	double sigma_min = 0.001;
	if (SL0(A, y, sigma_min, s))
	{
		cout << "传感矩阵为：" << endl << A << endl << endl;;
		cout << "生成向量为：" << endl << y << endl << endl;;
		cout << "重构出更高维的原始向量的稀疏表示为：" << endl << s << endl << endl;;
	}
	else
		fprintf(stderr, "Error in calling SL0 function.\nsigma_min = %f", 
				sigma_min);
	system("pause");
	return 0;
}

验证结果为

SL0算法的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
bool MyDelta(const Mat s, const double sigma, Mat &delta)
{
	for (int i = 0; i < s.rows; ++i)
		for (int j = 0; j < s.cols; ++j)
			delta.at<double>(i, j)  = s.at<double>(i, j) *
			exp(-1 * s.at<double>(i, j) * s.at<double>(i, j) / (2 * sigma * sigma));
	return true;
}
bool SL0(const Mat A, const Mat y, const double sigma_min, Mat &s)
{
	double iteration_factor = 0.5;
	double lamdba = 0.1;
	double sigma;
	int mu_0 = 2;
	int L = 3;
	
	//A_pinv为矩阵A的伪逆
	Mat A_pinv;
	invert(A, A_pinv, cv::DECOMP_SVD);
	
	//向量s和增长序列sigma的初始化
	s = A_pinv * y;
	double minVal, maxVal;
	minMaxLoc(s, &minVal, &maxVal);
	sigma = abs(minVal) > abs(maxVal) ? abs(minVal) : abs(maxVal);
	sigma *= 2;
	//到达指定的停机准则就退出，siama_min越小，重建结果越精确
	while (sigma > sigma_min)
	{
		//迭代下降法迭代L次
		for (int i = 0; i != L; ++ i)
		{
			//delta为梯度下降方向
			Mat delta = Mat::zeros(s.size(), s.type());
			if (MyDelta(s, sigma, delta))
				delta += 2 * lamdba * (A.t() * (A * s - y));
			else
				fprintf(stderr, "Error in calculating delta");
			s = s - mu_0 * delta;		//梯度方向更新
			s = s - A_pinv * (A * s - y);		//约束正交投影
		}
		//迭代过程中，误差所占权重逐渐减小，自适应的调整lamdba和siama的值
		sigma = sigma * iteration_factor;
		lamdba = lamdba * (1 / iteration_factor);
	}
	return true;
}